Los puentes de corriente alterna son más versátiles y en consecuencia tienen más aplicaciones que los puentes de C.C. Se usan en medidas de resistencias en C.A., inductancia, capacidad e inductancia mutua, en función de patrones conocidos y relaciones conocidas de elementos.
Su forma básica consiste en un puente de cuatro ramas, una fuente de excitación (alterna) y un detector de cero (audífono, amplificador de C.A. con osciloscopio, etc.). Para bajas frecuencias se puede utilizar la línea de potencia como fuente de excitación; y a altas frecuencias se puede utilizar un oscilador.
Puente de Schering:
 Se usa mucho para medir capacidad y
el factor de potencia de los capacitores. Se
lo puede considerar como una modificación del puente de relación de
resistencias, en la que la resistencia de perdida R4
del capacitor que se ensaya C4 se equilibra por el capacitor variable C3 mas bien que con el patrón de
capacidad C.
Se usa mucho para medir capacidad y
el factor de potencia de los capacitores. Se
lo puede considerar como una modificación del puente de relación de
resistencias, en la que la resistencia de perdida R4
del capacitor que se ensaya C4 se equilibra por el capacitor variable C3 mas bien que con el patrón de
capacidad C.
Ecuaciones
que describen el equilibrio de este puente:
Se
usa para medir capacitancias siendo esta su característica principal.
Puente de MAXWELL:
Una red en puente de CA en la que una
rama está compuesta de una inductancia y una resistencia en serie; la opuesta,
de un condensador y una resistencia en paralelo; y las otras dos ramas, de resitencias
(figura).
Se usa para la medida de inductancias (en
función de un condensador conocido) o capacidades (en función de una
inductancia conocida).
Escribiendo la ecuación en términos de Zx (impedancia de la rama desconocida)
se obtiene:
Al escribir utilizando la admitancia Y1:
Zx = Z2*Z3*Y1
Observando a la figura se obtiene que:
Donde w es la frecuencia angular (2pf). Sustituyendo estos valores da:
Cuya parte real es:
Y la imaginaria:
Lx = R2*R3*C1
Cabe aclarar que las resistencias se expresan en ohms, las inductancias en henrys y las
capacitancias en faradios.
Limitaciones:
El puente de Maxwell se limita a la medición de Q medio (1<Q<10), puesto que los ángulos de fase de R2 y R3 suman 0° y la suma de los ángulos de las ramas 1 y 4 también será 0°, por lo tanto el ángulo de una bobina de Q alto sería cercano a +90°, pero el ángulo de fase de la rama capacitiva debería estar en –90° lo que significaría R1 muy grande lo que es poco práctico; por esta razón, para estos valores de Q se utiliza el puente de Hay.
Para Q<1 existen problemas de convergencia debido a la aparición del denominado equilibrio deslizante por valores de Q bajos (se genera una interacción entre los controles). El procedimiento normal para equilibrar el puente de Maxwell consiste en ajustar R3 hasta que obtener el equilibrio inductivo y luego ajustar R1 hasta obtener el equilibrio resistivo, repitiéndose este proceso hasta el equilibrio definitivo.
Puente de Hay:
 Como primera característica de este puente, se puede mencionar su utilización para la medición de inductancias. En la figura se observa la configuración clásica del puente Hay. A primera vista este puente no difiere demasiado de su equivalente de Maxwell, salvo que en esta ocasión el capacitor C1 se conecta en serie con la resistencia R1, por lo tanto para ángulos de fase grandes la resistencia R1 debe tener un valor muy bajo. Es esta pequeña diferencia constructiva la que permite su utilización para la medición de bobinas de Q alto (Q>10).
Como primera característica de este puente, se puede mencionar su utilización para la medición de inductancias. En la figura se observa la configuración clásica del puente Hay. A primera vista este puente no difiere demasiado de su equivalente de Maxwell, salvo que en esta ocasión el capacitor C1 se conecta en serie con la resistencia R1, por lo tanto para ángulos de fase grandes la resistencia R1 debe tener un valor muy bajo. Es esta pequeña diferencia constructiva la que permite su utilización para la medición de bobinas de Q alto (Q>10).
Si se sustituyen los valores de impedancias de las ramas del puente en la ecuación general de equilibrio de los puentes de CA, se obtiene:
Sustituyendo los valores anteriores en la ecuación de equilibrio:
Si se distribuye:
Separando los términos reales de los imaginarios:
Como en ambas ecuaciones están presentes los términos Lx y Rx, se
deben resolver simultáneamente, entonces:
Como se puede observar en las expresiones tanto la inductancia como la resistencia desconocida se encuentran en función de la velocidad angular w, por lo tanto sería necesario conocer con exactitud la frecuencia de la fuente de voltaje.
Observando la siguiente figura:
Si se reemplaza en las igualdades, se obtiene:
Para Q>10, el término (1/Q^2 ) < 1/100, por lo tanto Lx es aproximadamente igual a:
R2*R3*C1
En resumen se puede decir que para la medición de inductores con Q alto (Q>10) se
debe utilizar el puente Hay. En el caso de inductores de Q bajo (Q<10) el método apropiado
es la medición a través del puente Maxwell.
Puente de Owen:
El puente Owen es ampliamente utilizado para la medición de inductores, más precisamente para aquellas inductancias con factor de calidad bajos (Q<1). Su configuración clásica se representa en la siguiente figura, y observando esta se puede remplazar la ecuación de equilibrio para los puentes de C.A
Z1*Z3 = Z2*Z4
Por lo tanto:
Si se igualan las partes reales e imaginarias, se obtiene:
Como se puede ver de las ecuaciones, el equilibrio del puente es independiente de la frecuencia, y como el término C1*R2 es conocido, dicho equilibrio depende exclusivamente de los elementos ajustables C3 y R3









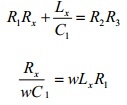





No hay comentarios:
Publicar un comentario